1955年,美国盛行答题积累奖金的电视节目,答题者通过连续答对题目来累计奖金池。而在电视外,庄家针对这个节目开设了答题者能否答对题目的赌盘,吸引了许多赌徒参与下注。
但是,节目在东海岸直播,西海岸则有直播延时,有赌徒便抓住了这个机会,利用延时提前通过电话得到了答题者答题情况,赶在西海岸直播前参与下注,从中套利。
受此启发,贝尔实验室的科学家约翰·拉里·凯利于1956年在《贝尔系统技术期刊》中提出了凯利公式:

“如果通信渠道的输入符号代表偶然事件的结果,在该偶然事件中,可以按照与其概率一致的赔率进行投注,那么一个赌徒就可以利用输入符号给他的信息,使他的钱以指数形式增长。”
论文中他以一个赛马模型提出了凯利公式的雏形:
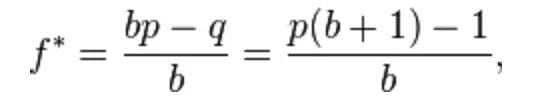
其中:
f* = 应该放入投注的资本比值
p = 获胜的概率
q = 失败的概率
b = 赔率
举个例子,如果一个赌博你有60%的获胜率(p=0.6, q=0.4),并且赔率是1赔2(b=2),则赌客每次下注的资金是 40% (计算方式:(b*p-q)/b)
当然,当初提出这个公式的凯利其实是为了通信学研究的,并不是很贴近实际投资场景。不过,它有一个变形:

其中:
f* = 应该放入投注的资本比值
p = 获胜的概率
q = 失败的概率
rW = 净利润率
rL = 净损失率
这个公式很关键,因为它使得计算投资利润最大化的本金数额成为可能。比如说,使用我们之前的MACD量化投资策略:
有1万元购买股票,10%的止盈点,10%的止损点,假设针对某只股票每次盈利的概率是7/8,此时rW=0.1, rL=0.1,那么每次交易我们应该投入 f=((7/8)*0.1 – (1/8)*0.1) / 0.1*0.1=7.5%。
也就是说,按照这个策略买股票,每次你只能投入本金的7.5%才能使利润获得最大化。
这个公式用Python来计算也非常简单:
def kelly(p, q, rW, rL):
"""
计算凯利公式
Args:
p (float): 获胜概率
q (float): 失败概率
rW (float): 净利润率
rL (float): 净亏损率
Returns:
float: 最大化利润的投资本金占比(%)
"""
return (p*rW - q*rL)/(rW * rL)
基本就是把公式照搬下来计算。
凯利公式看起来真的很不错,不过,请大家注意了,量化投资中的获胜概率,比如我们上述计算中的盈利概率: 7/8,是基于某只股票的历史数据推测出来的,历史并不代表未来,因为未来是不可知的,我们只能说这只股票,在过去,表现的不错。
所以,模型永远只是一个近似的替代,并不能说明一切,凯利公式也是一样,如果凯利公式告诉你,要放大仓位,你可要三思,万一发生黑天鹅事件,分分钟教你做人,如果你还上了杠杆,那就要上人生最重要的一堂课了。
我们经常会认为凯利公式所针对投注比例是全资产,事实上,我更喜欢将凯利公式所针对的投注比例当做是你可承受损失的资产。
比如你有100万,你能承受10万的损失,那么这10万就能拿来根据凯利公式进行投资,因为这是最保险,能让你心情不那么痛苦的做法。
不要贪,很重要。
我们的文章到此就结束啦,如果你喜欢今天的Python 实战教程,请持续关注Python实用宝典。
有任何问题,可以在公众号后台回复:加群,回答相应验证信息,进入互助群询问。
原创不易,希望你能在下面点个赞和在看支持我继续创作,谢谢!
Python实用宝典 (pythondict.com)
不只是一个宝典
欢迎关注公众号:Python实用宝典


评论(0)